You hear this a lot, the idea that only winners and losers exist in a market. This notion has always sat with me as overly simplistic and not a fair or true picture. Hence, I wanted to dig a bit deeper into this idea with a bit of a case-by-case example.

This is an important question to grasp because if true, it makes the case for investing a hard one. It is an even harder case to make for the smaller investor who does not have a team of analysts and money to put into research backing them up.

So, while it seems like a bit of an ‘out there’ question, it is a very important one to answer in order to justify even bothering with investing. We will walk through a few ‘case-studies’.

The Simplistic Case: Two Participants and One Stock

The answer here is an obvious one: Investing is a zero-sum game. Obviously though, markets are far more complex than this particular case, but we will walk through it regardless.

Participant 1 (P1) currently holds a stock at $1 and sells it to Participant 2 (P2) at $1. If the stock goes up, P1 loses because they sold too early. If it goes down, P2 loses because they hold a losing investment. So, no matter the outcome, in a two-person market, there is always one winner and one loser.

Case 2: Three Participants and One Stock

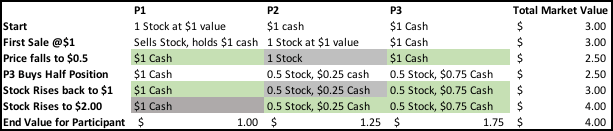
This is where the zero-sum claim starts to go off the tracks. We will let the above table do most of the talking here but the scenario goes along the lines of this:

P1 holds the stock and sells it to P2 at $1. The stock then falls by 50% and P3 sees value and decides to buy half of the stock. The share rises back to $1 and subsequently rise even more to $2. Cells shaded in green are the winners in each scenario and cells shaded in grey are the losers.

Once a scenario takes place, it gets harder to determine if P1 is a winner or loser. In theory, P1 is a loser for not buying at $0.5 and for selling in the first place, once it doubles in value. But P1 still gets their money early on, feeds their family, pays their bills and maybe even invested that dollar in a risk-free bond to generate some interest. So, one could argue, that when the market goes back to $1 and further to $2, all participants are winners (P2 made a bad decision by selling half at $0.5 but gets back to break even and made the ‘right’ decision by not selling out in full).

Admittedly, an investor could devise any mix of situations to show if investors win or lose. But, it is easy to see that in a world where there are multiple participants with assets that vary in value, it is possible for multiple winners to exist. It also paints the picture very quickly that in reality, the zero-sum example of one winner and loser to every transaction is oversimplified.

Case 3: Initial Public Offering (IPO)

We will go back to a simpler example here. Let’s say ‘Zark Muckerberg’ starts a company from scratch and wants liquidity so they take it public in a two-person market consisting of Zark and P1. Zark builds the business, continues to run it and sells half of it to P1. The company then doubles in value. P1 wins and Zark wins. The pessimist may point out that Zark is a fool as he sold half of his company at half of what it was worth but this does not account for the fact that overall, the total market is better off and Zark also has gained liquidity on what was likely a portfolio concentration issue.

Case 4: Continually trending up market

What about another case where markets continue to rise over the long term. Even only two investors selling a stock back and forth to one another can still both be winners if the general trend of the stock is upwards. An investor can own a stock at $1, sell it at $2, buy it back at $4 and sell it again at $6 and still be wealthier than when they started.

Yes, in a black and white world, every time the participant sold the stock, it means he lost to the buyer, because it continued to go up, but it does not make it an outright loss. For a reader that thinks this is an unrealistic scenario, we would actually argue that this is the most realistic scenario as the general trend of equity markets over the long-term has been up.

Case 5: Different investors have different needs

This is likely the most nuanced but most important point. The ‘zero-sum’ theory with investing assumes that every individual has the exact same goal which is to maximize profit. This is fine and an important assumption in textbooks but is quite simply not the case in the real world.

Investors have differing time frames, goals, and needs. It is easy to envision a scenario where an ultra-high net worth investor (UNHW) is happy to pay a premium for a dividend stock that gives them a near-certain tax-efficient dividend yield in perpetuity from a retiree that needs the cash. In one case, the UNHW investor is investing for the next generation, or the generation after that while the retiree is focused on paying the rent. Both parties get what they want/need, regardless of who gets the better or right price.

To the same point, a retiree may need to sell a high growth stock with great potential that has embedded gains already due to the volatility. A young investor with a long timeframe could buy it and use the potential future gains for their own retirement.

The point here is that investing is not just about making decisions based on expected return (not to mention that expected returns are not true returns) but making decisions that meet specific individuals' or institutions' needs and wants.

If we take a scenario where there are a set number of participants, a known and unchanging intrinsic value on a set of investments, a homogenous investor base, and a world where no additional value can be created (like growth in a business), then sure, we can see a scenario where investing is indeed a zero-sum outcome with one winner or one loser. Fortunately, the above criteria could not be further from reality.

To be honest, as I worked through this question, I expected it to be difficult to prove one way or another but the more thought that went into this question it seemed to become all the more clear that the zero-sum outcome for investing is a large oversimplification of things.

The unfortunate thing about this is that it is a claim I hear time and again and likely does far more harm than good. For an individual just thinking about investing and hearing or reading a headline that equates to something like ‘50% of people who invest will lose their money’; that can be a scary hurdle to overcome and be enough to discourage someone from the outset.

For any investors on the sidelines, trying to determine if they should invest or not, hopefully they can now cross the ‘zero-sum’ claim off as the reason that keeps you from entering the market. After all, not investing over the long-term could be the most costly outcome of all.

Have a question? Sign up for free to ask 5i's Research Team your top stock or investing question, plus get instant access to Canada's top stocks, three model portfolios, and over 62,000 answered investments questions. Get your free 5i Research Trial here.

Article by Ryan Modesto - CEO of 5i Research

See Ryan's previous articles here:
When to Sell a Stock for Portfolio Optimization

When to Sell a Stock for Fundamental Reasons